Playing Fasttracker 2 .XM files in Javascript
Nov 9, 2015
What is this thing?
Hit the play button above and it will play music; specifically, music composed with (or at least, compatible with) a program released in 1994 called FastTracker 2; this is a Javascript homage I wrote in a fit of nostalgia. The source code is on GitHub if you'd like to check it out.
Hit "Load" to load a few other .XMs I have handy on my web host, or drag and drop an .xm from your computer onto the player window.
FastTracker 2 looks like this:
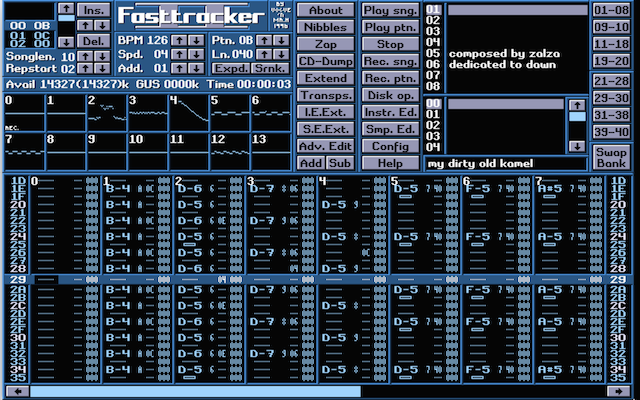
I using the original font to render a pastiche of the FT2 interface above.
.XM files
The ubiquitous .MOD music file format originated on the Commodore Amiga in the late 80s. It was more or less designed around the "Paula" chip inside the Amiga which plays four 8-bit PCM channels simultaneously. It is fairly amazing what artists are able to accomplish in just four voices; I've converted a few of Lizardking's old four-channel .MODs to .XM format so they can be played in the player above; try them out with the load button above.
FastTracker 2's .XM (eXtended Module) format was created as a multi-channel extension to .MOD in the 90s; it was written by PC demo group Triton. There were other contemporaneous multi-channel MOD-type music trackers, like ScreamTracker 3's .S3M and later Impulse Tracker's .IT. Nearly all PC demos and many games in the 90s and early 2000s played music in one of these formats.
Underneath the hood, it's several (14 in the case of the default song that comes up here) channels independently playing samples at various pitches and volume levels, controlled by the pattern which is what you see scrolling above.
Patterns are a lot like assembly language for playing music, complete with a slew of hexadecimal numbers and opaque syntax, except they are laid out like a spreadsheet rather than a single column of instructions. Each cell contains notations for playing or releasing a note with a certain instrument, optionally modifying the volume, panning, or pitch with effects.
Every sound that is played is one of the samples, shown at the top of this page as little waveforms and numbers in the table below the pattern. The idea is that the musician would record an instrument, like a piano or a bass, at a certain note, and then we play them back at higher or lower speeds to change the pitch.
Theoretically each sample has a name like "piano" or "bass", but in practice, musicians tended to erase those and write messages instead. Later trackers would add a song message field to avoid abuse of the instrument list.

In the above example, we are about to play an E note in octave 5 with instrument number 2 on the first channel, and in the second channel we play the same note an octave higher with the same instrument, except we also lower the volume to 0x2C (maximum volume is 0x40, so this is between a half and 3/4ths full volume). The second channel is also going to play with effect 0, which is an arpeggio, switching between 0, 0x0c or 12, and 0 semitones higher -- meaning it's going to rapidly play a sequence of E-6, E-7, E-6, and repeat.
Tracker programs don't have any knowledge of the musical scale, so they always render accidentals as sharps, e.g. C#4 instead of Db4.
XM instruments go beyond .MOD samples in that they include volume and panning envelopes, and can have multiple different samples per instrument -- so you could record various piano notes and use a recording closest to the note you're playing rather than stretching a sample several octaves, which sounds bad. I only render the first sample per instrument in the table above though.
In .MOD-derived formats, each row of pattern data is played at a certain rate controlled by the speed and BPM which have a sort of tangential relationship to the terms you may be familiar with. speed controls the row speed in ticks, and BPM controls how long ticks are. A tick is defined as 2500/BPM milliseconds.
Typical values are BPM=125 and speed=6, corresponding to 2500/125 = 20ms per tick, or 50 ticks/second; and 50/6 = 8.333 rows per second. If we assume the downbeat happens every four rows then it works out to 125 beats per minute. But if speed is 5 then it's 150 beats per minute, so we can't really take the terms at face value.
Each tick we process effects -- modifications to the volume or pitch of a note. Effects are represented by three hexadecimal digits: the effect type (first digit) and parameter (second two digits). In XM the effect type goes beyond the hex digits and goes all the way from 0-9 and A-Z.
Examples include arpeggio (switching between three notes really fast; effect 047 plays a major chord), portamento (sliding from one note to another, like a trombone does; effect 1xx slides up 2xx down, and 3xx to a specific note), vibrato (vibrating the pitch up and down; 4xx), or ramping the volume up or down (Axy). If you watch closely while the song is playing you can try to work it out.
The intracacies of how effects work -- some affect the song playing as a whole, some happen only on the first tick of a row, some only on every tick except the first one in a row -- could be its own long and not very interesting article, so I'll leave out the details. There are decent but mutually contradictory resources online.
Real-time Audio Synthesis in Javascript
The webkitAudioContext element was introduced to HTML a while back, and is
now available in the standard as AudioContext. The API is fairly flexible, and
one of the things you can do with it is get a Javascript callback which writes
samples more or less directly to the output device, just like we used to do
with DMA loop interrupts back in the day. It's called createScriptProcessor.
You can be up and running making all kinds of noise in a jiffy:
function InitAudio() { // Create an AudioContext, falling back to // webkitAudioContext (e.g., for Safari) var audioContext = window.AudioContext || window.webkitAudioContext; var audioctx = new audioContext(); // Create a "gain node" which will just multiply everything input // to it by some constant; this gives us a volume control. gainNode = audioctx.createGain(); gainNode.gain.value = 0.1; // master volume // Create a script processor node with 0 input channels, // 2 output channels, and a 4096-sample buffer size jsNode = audioctx.createScriptProcessor(4096, 0, 2); jsNode.onaudioprocess = function() { var buflen = e.outputBuffer.length; var dataL = e.outputBuffer.getChannelData(0); var dataR = e.outputBuffer.getChannelData(1); // dataL and dataR are Float32Arrays; fill them with // samples, and the framework will play them! }; // Now, form a pipeline where our script feeds samples to the // gain node, and the gain node writes samples to the // "destination" which actually makes noise. jsNode.connect(gainNode); gainNode.connect(audioctx.destination); }
Your onaudioprocess function will be called back whenever new samples are
needed to fill the output buffer. With a default samplerate of 44.1kHz, a
4096-sample buffer will expire, and thus your callback will be called, every
~92 milliseconds.
Our goal is to fill this buffer up with the sum of each channel's output waveform. Each channel outputs a sample playing at a certain frequency and at a certain volume. And during a tick, the sample frequency and volume is constant1. Between ticks, we recompute the channel frequencies, volumes and envelopes; and on ticks which are even multiples of the current speed value (3 in the example below), we read a new row of pattern data -- notes, instruments, effects, etc.
The output is just the sum of the individual channels2 for each sample.

When we're done, the output will be laid out something like this:

In this example, a tick is 20ms and our output is playing at 44.1kHz, so a tick
is 882 samples. Of course, ticks don't evenly divide sample buffers, and the
AudioContext specification requires you to use buffer sizes which are powers
of two and ≥ 1024. So when we render samples to our buffer, we may have to
play a partial tick at the beginning and end.
So in our audio callback, we figure out how many samples are in a tick, and fit them into the output buffer, and add up each channel's data within a tick. It looks like this3:
var cur_ticksamp = 0; // Sample index in current tick var channels = [ ... ]; // Channel state: sample num, offset, freq, etc function audioCallback(e) { var buf_remaining = e.outputBuffer.length; var dataL = e.outputBuffer.getChannelData(0); var dataR = e.outputBuffer.getChannelData(1); dataL.fill(0); // (see footnote 3) dataR.fill(0); var f_smp = audioctx.sampleRate; // our output sample rate var ticklen = 0|(f_smp * 2.5 / xm.bpm); // # samples per tick var offset = 0; while(buf_remaining > 0) { // tickduration is the number of samples we can produce for this // tick; either we finish the tick, or we run out of space at the // end of the buffer var tickduration = Math.min(buf_remaining, ticklen - cur_ticksamp); if (cur_ticksamp >= ticklen) { // Update our channel structures with new song data nextTick(); cur_ticksamp -= ticklen; } for (var j = 0; j < xm.num_channels; j++) { // Add this channel's samples into the dataL/dataR buffers // starting at <offset> and spanning <tickduration> samples mixChannelInfoBuf(channels[j], offset, offset + tickduration, dataL, dataR); } offset += tickduration; cur_ticksamp += tickduration; buf_remaining -= tickduration; } }
Note frequencies
In .MOD derivatives, notes at C-4 (that is, a C on octave 4) are played at a
samplerate of 8363Hz. Everything is relative to that; an octave higher, for
instance, would be 16726Hz -- twice the frequency. For each semitone up, we
effectively multiply the frequency by the twelfth root of two. In general, the
frequency can be computed by 8363 * Math.pow(2, (note - 48) / 12.0). note
here is the note number in semitones, starting at 0 for C-0 and going up to 95
for B-7.
To support fine tuning, vibrato, slides and so forth in the XM format, effects modify the note "period" which is not a period but 1/16th of a (negative4) semitone. Also, each sample has a coarse and fine tuning offset which are added on when we compute the play frequency.
Resampling
mixChannelIntoBuf's job is to write a sample played at a certain frequency
onto a buffer which is played at the output frequency, usually 44.1kHz. It
turns out that playing a sample recorded at a different frequency from the
output frequency is a surprisingly nontrivial problem.
From the Nyquist-Shannon theorem, we know that our original sample only contains frequencies less than or equal to half the original sample rate. So ideally, when we play it back at the new frequency, the same set of frequencies should be played.
In practice, though, without using a "brick wall" or "sinc" filter, we're going to end up with some spurious harmonics due to the aliasing phenomenon. The only way to avoid that requires a convolution as long as the original sample. In other words, it's computationally expensive.
Also, since the original .XM players didn't do anything fancy, it's also typically unnecessary.
It turns out that if we use advanced resampling techniques to eliminate unwanted alias harmonics, many songs5 sound pretty bad. The original hardware and software that played these either used "zero-order hold" -- just output the sample closest to the interpolated time -- or "first-order hold" -- interpolate between the surrounding samples.
I compromised with a very simple implementation that I think sounds pretty good. I use a combination of zero-order hold and a per-channel two-pole low-pass filter, which has very low implementation complexity. I will leave the details out here.
Either way, we compute the speed at which we proceed through the sample, which is the ratio of the playback frequency to the output frequency:
function UpdateChannelPeriod(ch, period) { var freq = 8363 * Math.pow(2, (1152.0 - period) / 192.0); ch.doff = freq / f_smp; }
The doff variable is the delta offset per sample. If we are playing at
exactly 44100Hz, then doff is 1, and we are just copying the sample into the
output.
Here's what zero-order hold looks like, omitting many details of sample looping or ending:
function mixChannelIntoBuf(ch, start, end, dataL, dataR) { var samp = ch.sample; for (var i = start; i < end; i++) { // Dumb javascript tricks: // we use a bitwise OR with 0 to truncate offset to integer var s = samp[0|ch.off]; ch.off += ch.doff; dataL[i] += ch.volL * s; // multiply by left volume dataR[i] += ch.volR * s; // and right volume if (ch.off >= ch.sample.length) { if (ch.sample.loop) { ch.off -= ch.sample.looplen; } else { return; } } } }
In practice I unroll that loop, compute how many samples I can generate before the sample ends or loops so I don't have to test in the inner loop, and also unroll short sample loops in memory.
The end result runs fast enough to play without hitches on my phone.
The main problem with zero-order hold is that it produces hard edges between samples, and so there are a lot of high pitched hisses and noise. As a result, I added an additional low-pass filter to each channel with a cutoff equal to half the playback sampling frequency.
Synchronized visualizations
It might seem reasonable that in order to show what's happening on the screen while you're hearing it, you need to use a really small buffer so that the latency between when we compute a sound buffer and when it plays is minimized. The problem with that is on a webpage, a low latency buffer can mean choppy audio as the browser might have better things to do than call your javascript audio callback within 20 milliseconds. It's pretty far from a realtime system.
But we actually don't care about latency at all; there are no external events changing the sound in an unpredictable way (other than pausing, which is handled separately). The code on this page is using a callback buffer size of 16384, over 300 milliseconds, and yet the oscilloscopes and patterns are updating at roughly the tick rate (~50Hz). How does that work?
Whenever I finish rendering a tick to the audio buffer, I push a visualization
state onto a queue, keyed by the current audio time in samples.
AudioContext has a currentTime attribute, which is the number of seconds
that audio has been playing since the context was created. On my audio
callback, I capture this and then add offset / f_smp to the time for each
tick. And then I push the first few samples of each channel, plus the current
pattern and current row, onto a queue. My rendering code just compares
audioctx.currentTime against the head of the queue and renders what comes
next.
var audio_events = []; function redrawScreen() { var e; var t = XMPlayer.audioctx.currentTime; while (audio_events.length > 0 && audio_events[0].t < t) { e = audio_events.shift(); } if (!e) return; // draw VU meters, oscilloscopes, and update pattern position // using various 2D canvas calls }
The patterns are rendered by calling drawImage on individual letters from
the original font image onto an off-screen canvas
every time a new pattern is to be shown, and then compositing that canvas onto
the screen above in order to highlight the currently-playing row.
End result
The player is also available here without the accompanying
article. By the way, you can load arbitrary XMs on the web by using an anchor
with a link, e.g. https://www.a1k0n.net/code/jsxm/#http://your.host.here/blah.xm
-- but only if the host sets a CORS (Access-Control-Allow-Origin) header.
I think what was most fun about playing .MODs and their ilk back in days of yore was that you could actually see how a complex piece of music is put together, and watch your computer perform it live. I wanted to recreate that experience. There are other web-based .MOD players now, like mod.haxor.fi, but I wanted to write my own just for fun.
It was fun. Though it isn't complete effects-wise, I couldn't be happier with how it turned out.
Footnotes
- The one exception being when the sample ends during the tick. ↩
- I've omitted the details of stereo, but we sum up the left and right channels independently. Panning is just a different volume on the left channel vs. the right channel. ↩
Array.fill()is not available in all browsers, so in practice I use a for loop to clear the buffer. And the buffer is not already cleared when it is passed to us; it may actually contain data from the previous callback. ↩- For historical reasons I won't go into here, .MOD effects modified the sample period, or inverse frequency, as making linear changes to it sounds more linear to the ear; but really, it's an approximation of the logarithmic scale the human ear actually hears. A log scale is used in .XM. So when we increment period in XM, we are stepping down 1/16th of a semitone. ↩
- Especially "chiptunes" -- songs with tiny looping square wave or triangle wave samples, to emulate simple vintage sound hardware chips. ↩